正弦波从采样到梅尔频谱图

本文内容为正弦波的采样, 加窗, 傅里叶变换和梅尔滤波, 将波形定为简单的正弦波是为了简化例子, 专注于每个变换所带来的数值上的变化, 以更好的理解整个过程, 为音频处理做铺垫.

注意: 文中FFT 部分只是列出了傅里叶变换的输出, 并没有解释为什么是这样的输出, 比如用torch.fft.fft()得到的是复数, 需要求模长, 并除以样本的一半, 才是正确的幅值等.这些都涉及到傅里叶变换的原理, 本系列文章暂时不涉及, 插个眼在这里, 万一以后有契机补充这部分内容也说不定.

所有代码的import

1
2
3
4
import torch
import torchaudio
import matplotlib.pyplot as plt
import numpy as np

采样

对频率为500 Hz 幅值为100 的正弦波进行5 个周期的采样, 分别设置采样率为1-6 倍原频率.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 正弦波的频率
f1 = 500
# 周期
T = 1 / f1
# 采样范围
TT = 5*T

fig, axes = plt.subplots(2, 3, figsize=(20, 10))

for i, ax in enumerate(axes.flatten()):
    # 采样率
    fs = f1 * (i + 1)
    # 采样点数
    N = int(fs * TT)
    print(f"f1 = {f1}, T = {T}, TT = {TT}, fs = {fs}, N = {N}")

    x = torch.linspace(0, TT, N)
    y = 100 * torch.sin( (2*torch.pi)*f1*x)

    # 原波形
    ax.plot(x, y)
    ax.set_xlabel("time")
    ax.set_ylabel("amplitude")
    ax.set_title(f"sample wave (fs = {fs})")

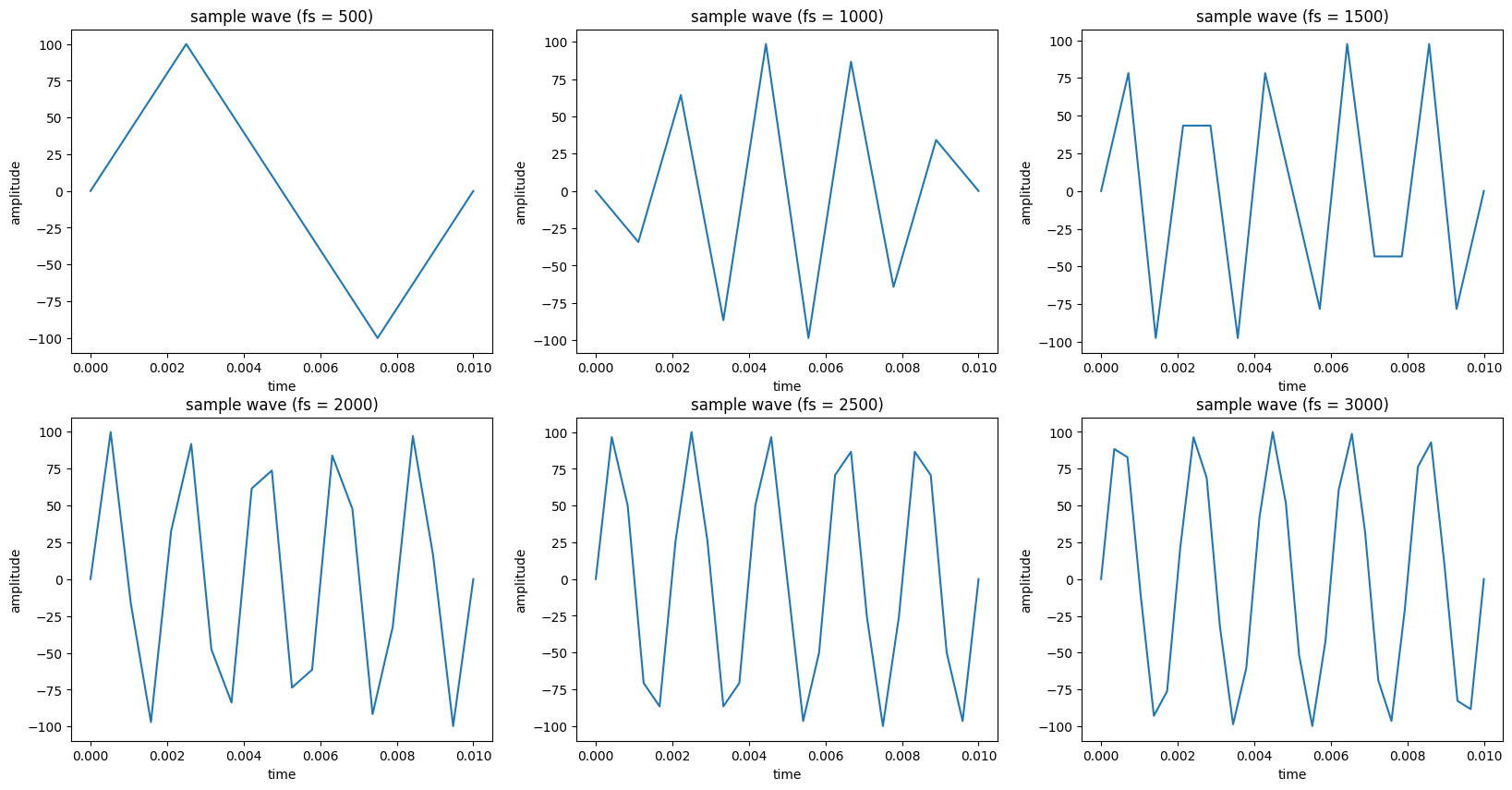
alt text
可以明显看到, 采样率越高越还原波形, 最少需要两倍原频率.

FFT

为了展示出FFT 的作用, 这里用了5 个不同频率和幅值的正弦波以及一个随机噪声, 采样率设定的比较高, 让波形看起来比较丝滑.后续处理都是基于这个波形, 前面采样部分只是起到一个演示作用.

下面直接画出FFT 前后的波形.需要注意的是, 在FFT 前我先把波形都归一化到了[-1, 1].至于为什么可能要看完本篇文章才能看得懂: 对于单个音频来说, 同个语句由于响度不一样大, 波形幅值会不一样, 但大致形状相同.到文章的最后输入模型的分贝值就会产生偏移, 这会给模型带来数值大小的困扰, 如果归一化就不会有这个问题.对于不同的语句音频, 归一化就是去除响度的干扰因素, 默认所有语句, 都一个响度.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# 第一个正弦波
# 正弦波的频率
f1 = 1000
# 周期
T = 1 / f1
# 采样范围
TT = 10*T
# 采样率
fs = 20000

N = int(fs * TT)

# 第二个正弦波
f2 = 300

# 第三个
f3 = 700

# 第四个
f4 = 7000

# 第五个
f5 = 5000

x = torch.linspace(0, TT, N)
# 直接相加
y1 = 70 * torch.sin( (2*torch.pi)*f1*x)
y2 = 50 * torch.sin( (2*torch.pi)*f2*x)
y3 = 20 * torch.sin( (2*torch.pi)*f3*x)
y4 = 60 * torch.sin( (2*torch.pi)*f4*x)
y5 = 80 * torch.sin( (2*torch.pi)*f5*x)
# 噪声
noise = torch.randn(N) * 100

y = y1 + y2 + y3 + y4 + y5 + noise
y = y1 + y2 + y3 + y4 + y5 
# 缩放到[-1, 1]
max_val = torch.max(torch.abs(y))  # 找到绝对值最大值
if max_val > 0:
    y = y / max_val  
print(f"max_val: {max_val}")

fig, axes = plt.subplots(1, 2, figsize=(20, 10))
axes = [axes]
# fig, axes = plt.subplots(2, 2, figsize=(20, 10))
# 原波形
axes[0][0].plot(x, y)
axes[0][0].set_xlabel("time")
axes[0][0].set_ylabel("amplitude")
axes[0][0].set_title("original wave")

# FFT
y_fft = torch.fft.fft(y)
y_fft = torch.abs(y_fft) / (N / 2)
x_fft = torch.linspace(0, fs, N)

axes[0][1].plot(x_fft, y_fft)
axes[0][1].set_xlabel("frequency")
axes[0][1].set_ylabel("amplitude")
axes[0][1].set_title("after FFT")

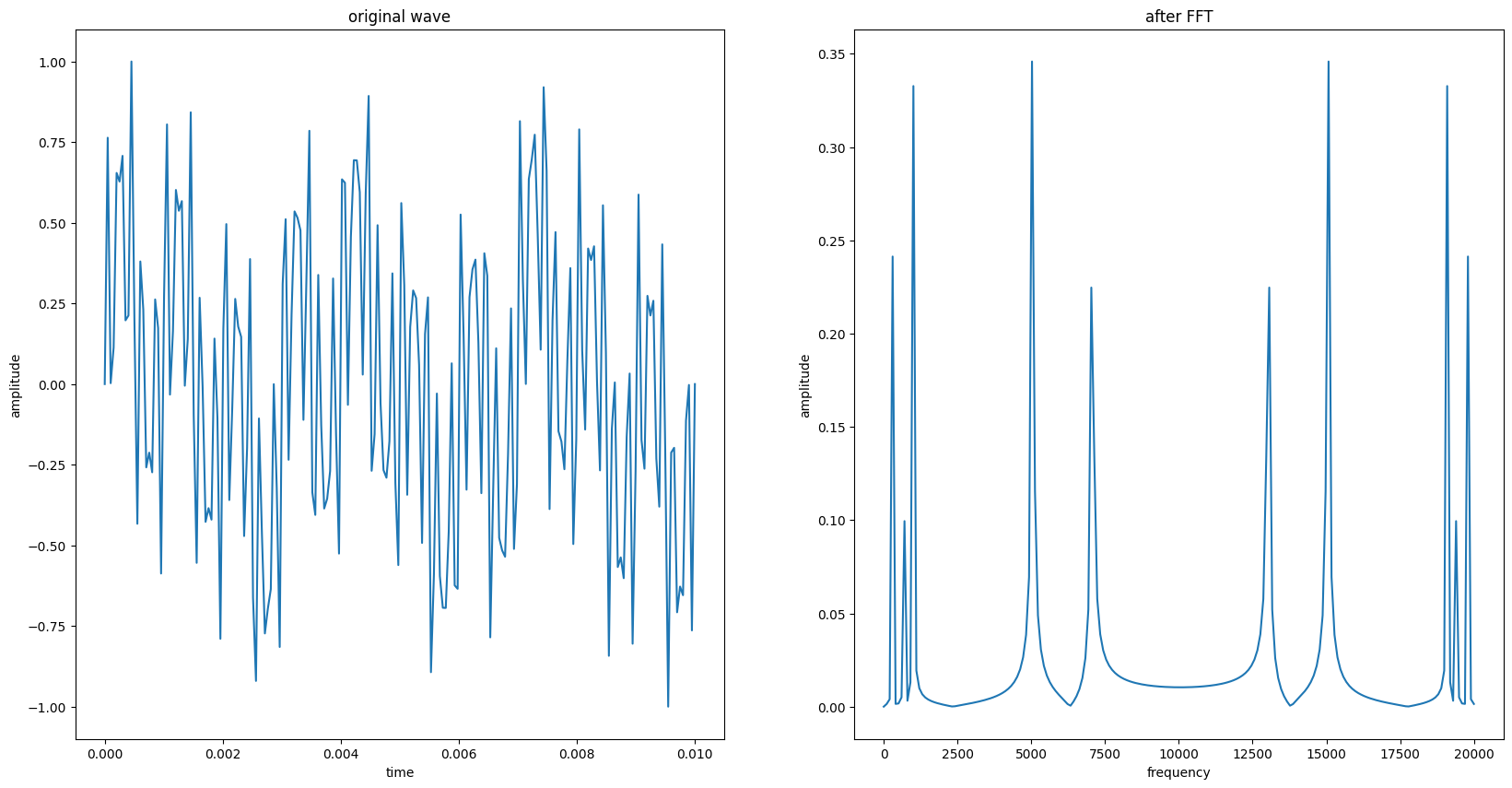
alt text

注意torch.fft.fft() 计算得到的是复数, 需要勾股定理求模长, 然后要除以一半的样本数, 这样得到的幅值才是符合原本的度量.

1
2
y_fft = torch.fft.fft(y)
y_fft = torch.abs(y_fft) / (N / 2)

原始波形的横坐标是时间, 纵坐标是幅值.
FFT 后的波形叫做幅值图, 它的纵坐标也是幅值, 但横坐标却是频率.点(x, y)表示, 在原始波形中, 频率为x 的正弦波分量的幅值是y .图(左右对称)左边有5个凸起, 分别对应5 个正弦分量.其中中频率为7000 Hz, 与5000 hz 的值为0.35 和0.225, 这如果没有进行归一化这两个值应该在60, 80 左右, 正好对应初始正弦分量的幅值.归一化就是线性除以了一个系数, 乘上这个系数,就可以变回60 和 80.

但是要画出幅值图可不像画出原始采样波形那样简单, 需要你知道FFT 的输出究竟是什么.

  • 横坐标的个数
    • 原始采样波形有多少个点(N), 那么个数就为N
  • 横坐标的单位与数值
    • 单位就是Hz, 因为其表示的是频率
    • 数值间隔, 也就是分辨率(interval 简称 I), 为: 采样频率(fs) / (横坐标个数(N) - 1)
    • 数值范围为0 到 采样频率(fs)
  • 纵坐标: 与原始采样波形一样, 表示幅值大小, 只是等比缩放了

一般只取幅值图的左半边, 因为它左右对称:

  • 横坐标的个数变为: (N // 2 + 1)
  • 横坐标的范围变为: (0 Hz 到 (N//2*I) Hz )
1
2
3
4
5
6
7
8
9
10
# 取一半
interval = fs / (N-1)
x_fft = torch.linspace(0, (N//2)*interval, N//2+1)
y_fft = y_fft[0:N//2+1]

fig, axes = plt.subplots(figsize=(20, 10))
axes.plot(x_fft, y_fft)
axes.set_xlabel("frequency")
axes.set_ylabel("amplitude")
axes.set_title("Keep half")

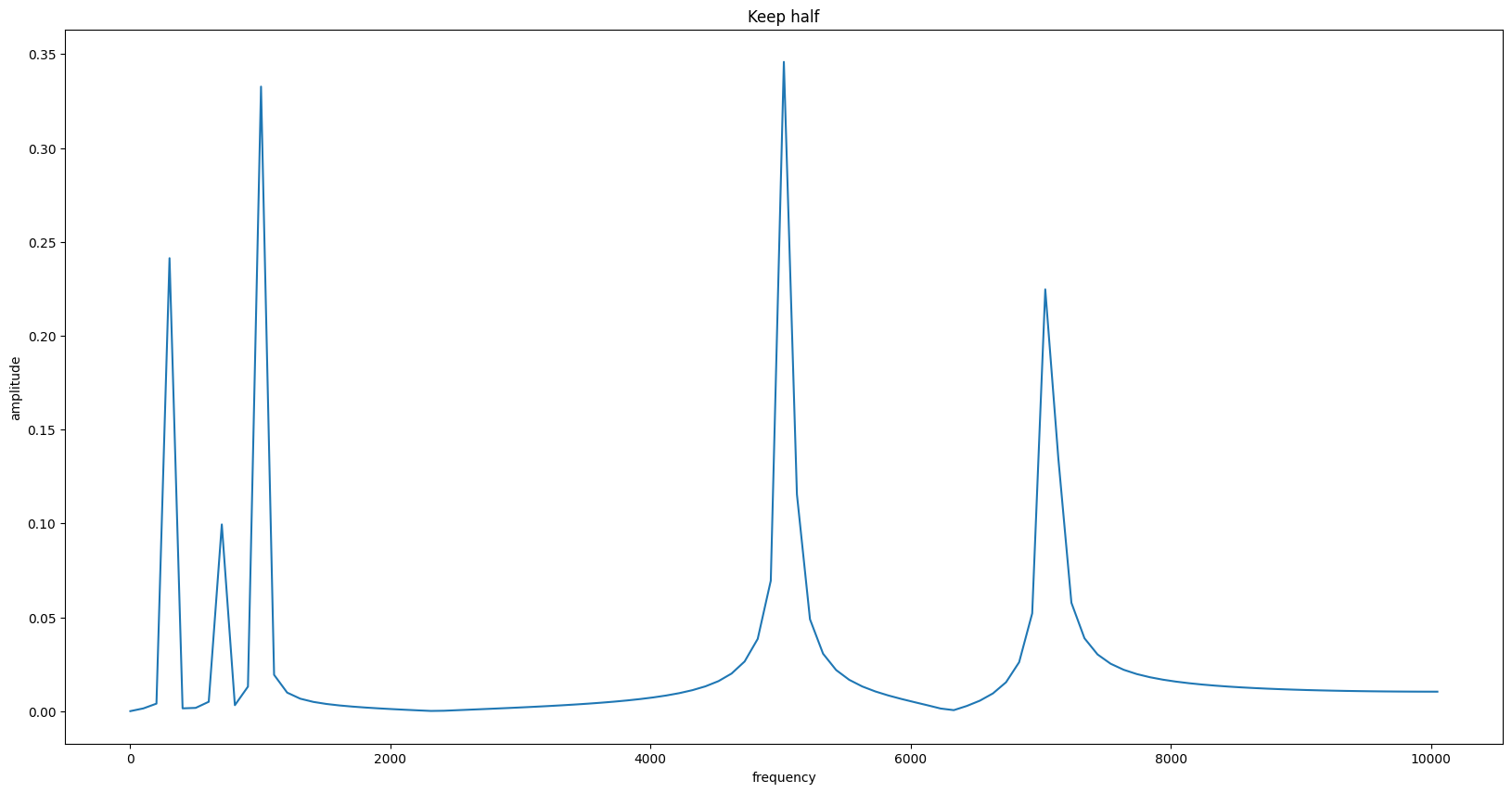
alt text
总的来看FFT 只能分析一半采样频率以内的频率分量, 而且采样点数越多, 分析的频率分量就越多频率间隔就越小.

功率谱

幅值谱的纵坐标表示幅值, 对于声波来说就是声压.将幅值平方即可转化为功率.
功率谱如下:

1
2
3
4
5
6
7
8
# 功率谱
y_pow = y_fft ** 2

fig, axes = plt.subplots(figsize=(20, 10))
axes.plot(x_fft, y_pow)
axes.set_xlabel("frequency")
axes.set_ylabel("power")
axes.set_title("power spectrum")

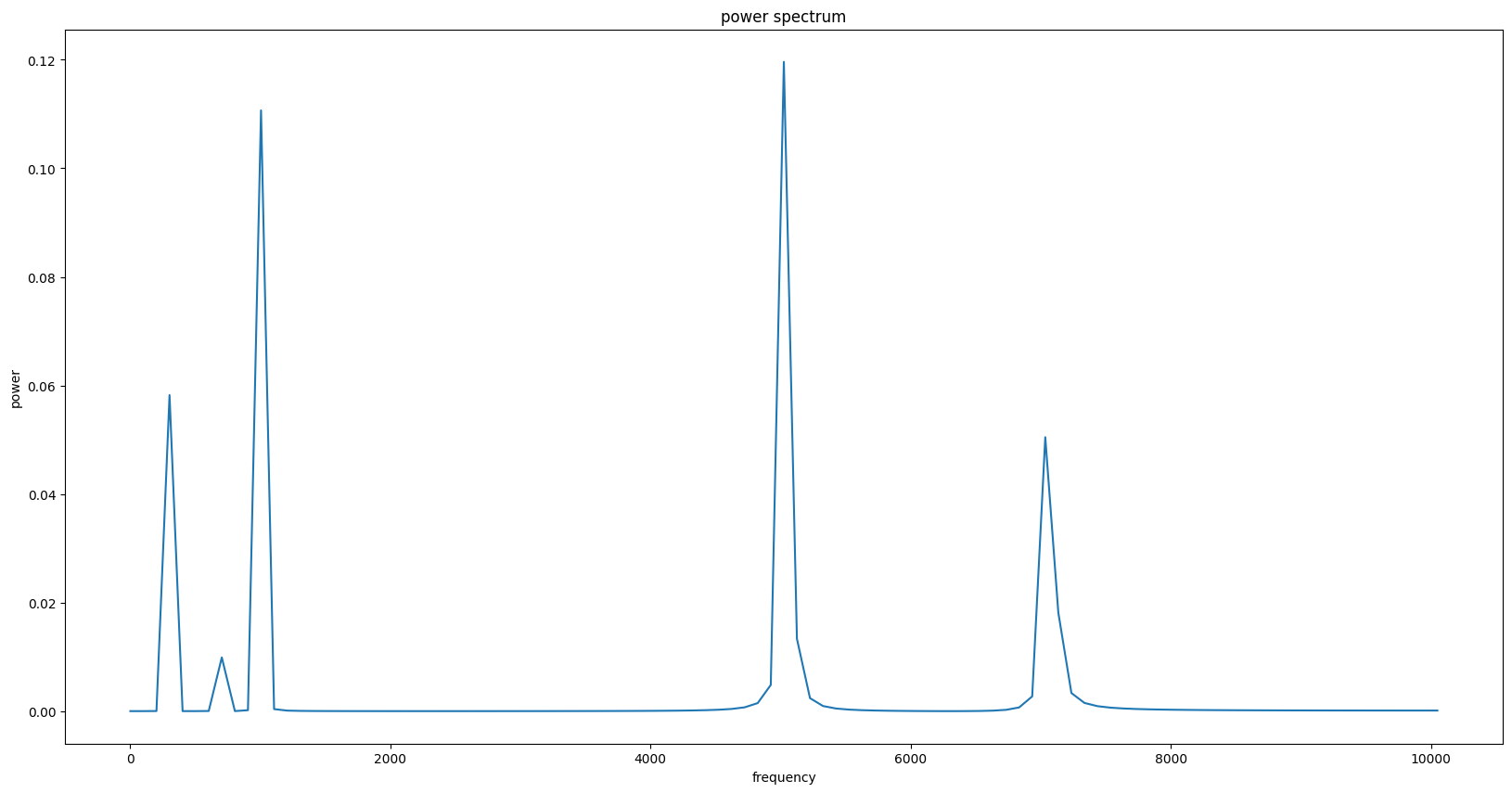
alt text
这个图的点(x, y) 表示频率为x 的正弦分量的功率为y.

梅尔滤波

这一步会将功率谱转化为梅尔频谱图, 将功率转化为能量.
如何进行转化呢? 就是将原功率谱与n 个等长的梅尔滤波器相乘再相加,得到长度为n 的梅尔频谱图.

得到梅尔滤波器

人耳对频率的感受是非线性的, 比如你会感觉1000Hz 与2000Hz 差别巨大, 但6000Hz 与 7000Hz 差距并没有这么大.梅尔频率与普通频率基本相同, 只是单位不一样, 前者为mel 后者为Hz.将普通频率转化为梅尔频率后, 1000ml 与2000ml 和6000ml 与7000ml 在听觉上的差距就一致了.
两者存在定量的转换公式:
alt text
计算梅尔滤波器的大致步骤:先在hz 单位下, 取一个最大频率和最小频率, 将它们都转化为mel 频率, 再根据mel 单位下的数值等距划分出中间多个数值.这样就得到了一个单位为mel 的等差数列频率, 再将这个等差数列转回hz 单位, 自然就不等差了, 但是符合人耳对频率差距的感知.
得到这些hz 数列后, 每三个数据, 创造一个三角滤波器, 每个三角滤波器可以对原功率谱进行滤波.
下面是计算梅尔滤波器的函数, 默认计算26 个梅尔滤波器(26 是前人总结的经验).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
"""
输入:
    n_fft: 窗口大小
    fs: 采样率
输出:
    x: FFT 后折半保留的单位为频率的轴
    mel_fliters: (num_fliters(26), fliter_size)
"""
def get_mel_fliters(n_fft, fs):
    # 计算mel 滤波器组
    def mel_to_hz(mel):
        return 700 * (np.exp(mel / 1125) - 1)
    def hz_to_mel(hz):
        return 1125 * np.log(1 + hz / 700)
    
    # 原幅值图X 轴范围
    # 分辨率
    interval = fs / (n_fft-1)
    # 保留点数: 总的FFT 点数除以二加一
    n_fft_reserve = n_fft // 2 + 1
    # 幅值图X 轴
    x = torch.linspace(0, interval*(n_fft_reserve-1), n_fft_reserve)

    # print("x:")
    # print(x)

    # 计算mel 频率桶
    # 低于300 Hz 人耳感受不到,不需要计算这部分的能量
    hz_min = 300
    # 保留的幅值图中最大的频率
    hz_max = x[-1]
    mel_min = hz_to_mel(hz_min)
    mel_max = hz_to_mel(hz_max)
    # 26 个滤波器需要28 个点
    mel_bins = torch.linspace(mel_min, mel_max, 28)
    # 来回转换有误差, 保证转回Hz 时不超过范围
    hz_bins = torch.clamp(mel_to_hz(mel_bins), max=hz_max, min=hz_min)

    # print("hz_bins:")
    # print(hz_bins)

    # 计算原x 轴与频率桶最相近的频率索引
    hz_indexs = []
    for hz_bin in hz_bins:
        temp_abs = torch.abs(x - hz_bin)
        temp_min = temp_abs.min()
        indexs = torch.where(temp_abs == temp_min)
        hz_indexs.append(indexs[0].item())
    # print("hz_index:")
    # print(hz_indexs)
        
    # 判断频率桶是否重复, 如果重复则无法正常创造梅尔滤波器
    hz_index_set = set(hz_indexs)
    if len(hz_indexs) > len(hz_index_set):
        print("hz bin 有重复")

    # 创建mel 滤波器
    mel_fliters = torch.zeros((26, len(x)))

    for index, fliter in enumerate(mel_fliters):
        left = hz_indexs[index]
        center = hz_indexs[index + 1]
        right = hz_indexs[index + 2]

        # 线性上升部分
        for i in range(left, center):
            fliter[i] = (i - left) / (center - left)

        # 线性下降部分
        for i in range(center, right):
            fliter[i] = (right - i) / (right - center)
        
    return x, mel_fliters

可视化滤波前后:
注意这由于杂波每次生成的都不一样, 所以画图的纵坐标需要稍微调整一下.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
fig, axes = plt.subplots(3, 2, figsize=(20, 10))
ax = axes.flatten()


# 26 个梅尔滤波器叠加
x, mel_fliters = get_mel_fliters(N, fs)
for fliter in mel_fliters:
    ax[0].plot(x, fliter)
ax[0].set_xlabel("Hz")

# 原波形
ax[1].plot(y_pow)
ax[1].set_ylim(0, 0.15) 

# 第2个滤波器
ax[2].plot(mel_fliters[1])

# 被第2 个滤波器滤波后的原波形
ax[3].plot(mel_fliters[1] * y_pow)
ax[3].set_ylim(0, 0.15) 

# 第6个滤波器
ax[4].plot(mel_fliters[5])

# 被第6 个滤波器滤波后的原波形
ax[5].plot(mel_fliters[5] * y_pow)
ax[5].set_ylim(0, 0.15)

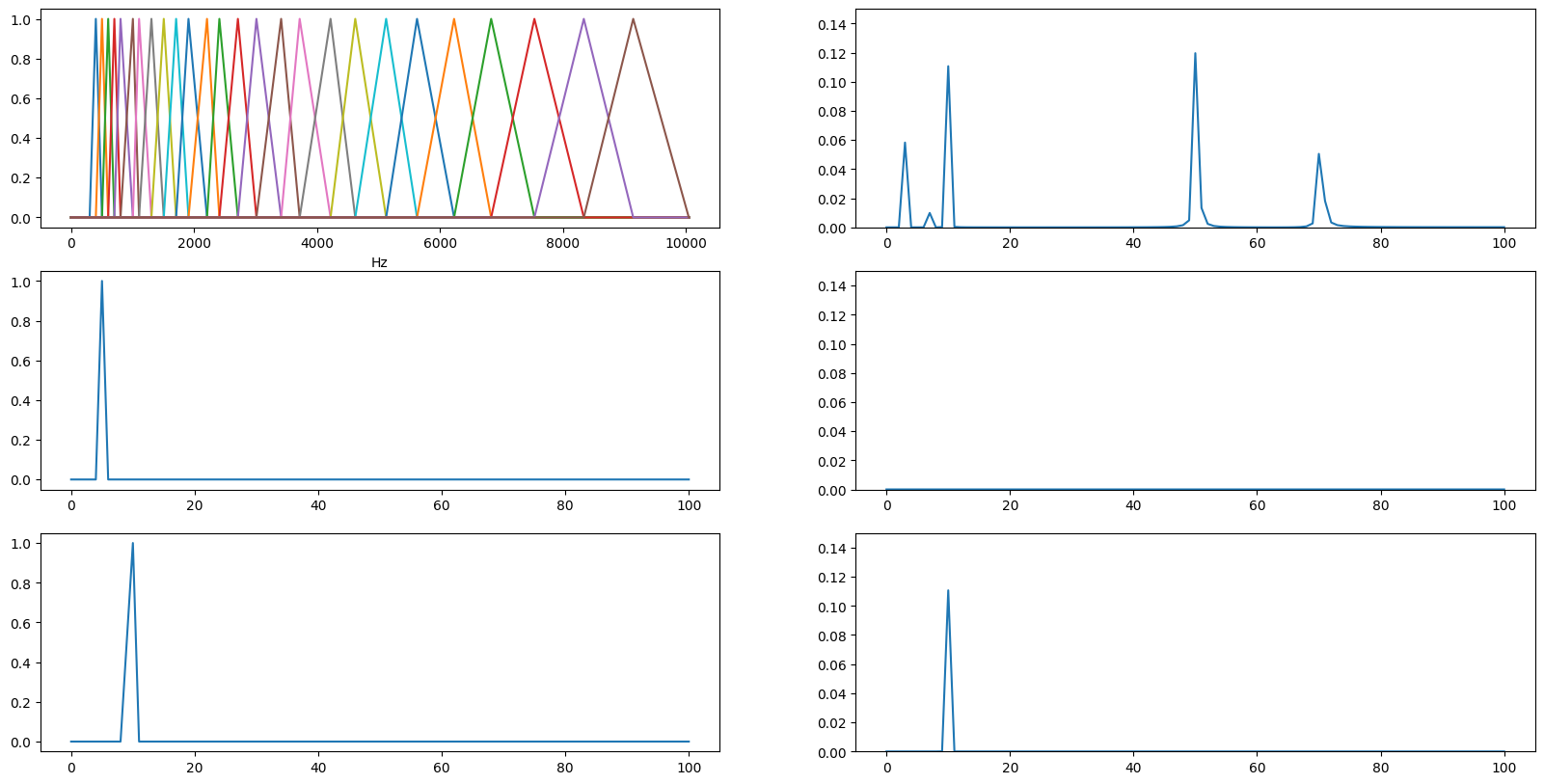
alt text

  • 左边三张图分别是
    • 26 个梅尔滤波器叠加
    • 第2 个滤波器
    • 第6 个滤波器
  • 右边
    • 原波形
    • 被第2 个滤波器滤波后的原波形
    • 被第6 个滤波器滤波后的原波形

说是滤波, 其实就是直接相乘.
滤波后的图像看起来就是三角形, 这是因为我们的原始波形太简单了,虽然加了噪声, 但是依旧很纯净.再下一篇的语音处理中, 就会复杂得多.

梅尔频谱图

用26 个滤波器对功率谱进行滤波会得到26 个向量, 向量中值代表的是功率, 如果将每个向量的值加起来,得到26 个值, 那么这些值代表的是什么呢, 能量.

1
2
3
4
5
6
7
8
9
10
11
12
fig, axes = plt.subplots(2, 1, figsize=(20, 10))

# 得到梅尔频谱图
mel_data = []
for mel_fliter in mel_fliters:
    mel_data.append((mel_fliter * y_pow).sum() )
axes[0].plot(mel_data)

# 将能量对数化, 转化成分贝
mel_data = torch.tensor(mel_data)
mel_data = 20*torch.log10(mel_data + 1e-10)
axes[1].plot(mel_data)

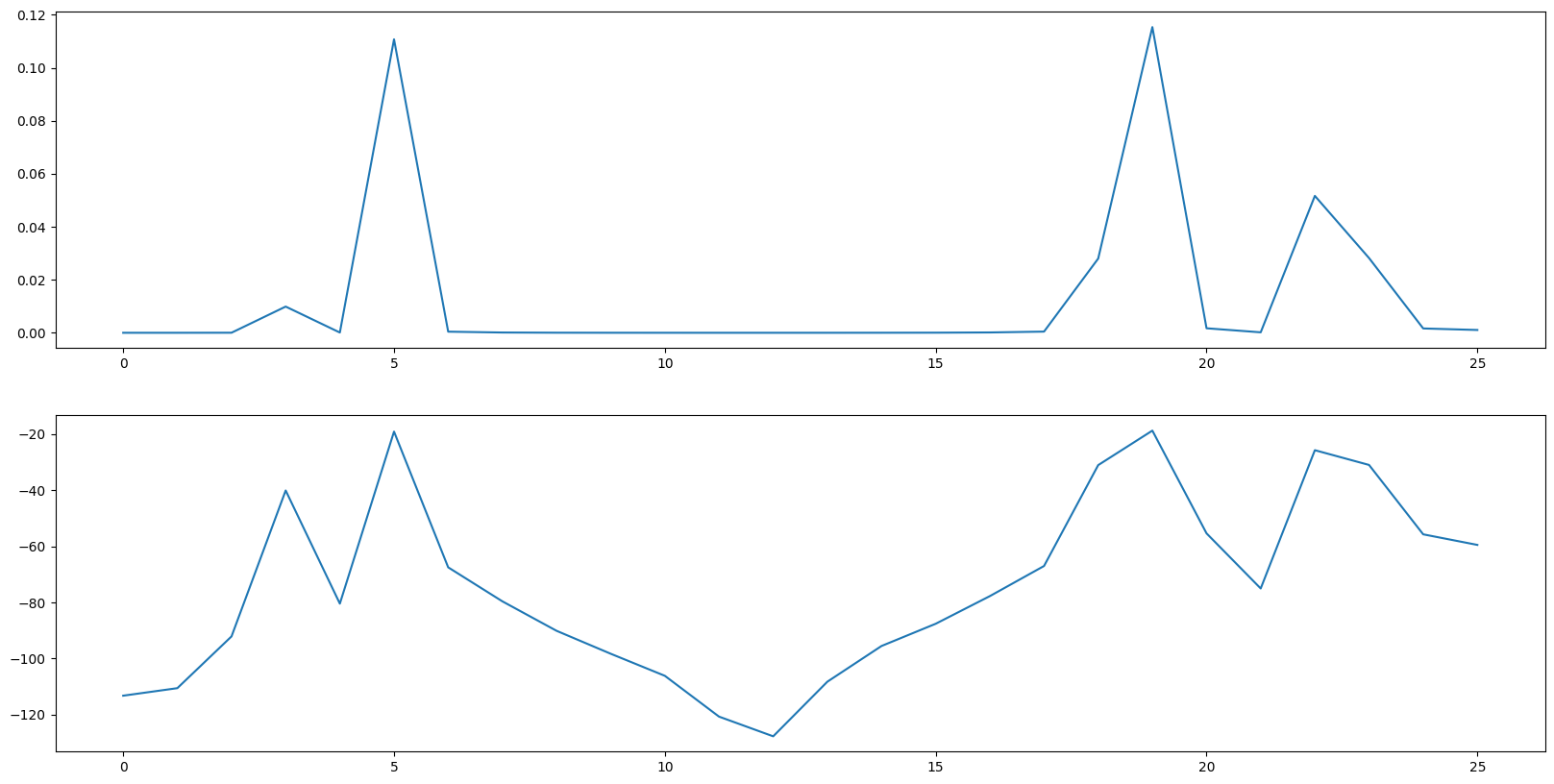
alt text

前面将hz 频率转化为mel 频率目的就让滤波的每个频率段落差值符合人耳听觉规律.这里将上图取对数得到下图也是同理.人耳对能量(响度)的感知也不是线性的, 人耳对响度（音量）的感知并不是线性的，而是更接近对数关系，即声音的主观响度随物理能量的变化呈对数增长。因此，对能量取对数可以使信号的表示更加符合人耳的听觉特性.
对数后的纵坐标从能量变成了加了对数并线性变换后的比例,分母是1, 所有的能量都在跟1 比, 如果其小于1 比例值最后就是负数.这个比例的单位就是分贝(dB).
所以我们得到了最终的梅尔频谱图, 它的横坐标是[0, 25], 代表原音频的26 个频率部分.它的纵坐标是对数比例, 单位是分贝, 代表各个部分能量与1 的比例.

但是我们通常不单独画一段音频的梅尔频谱图, 而是将时间连续的音频分别计算梅尔频谱图, 再画到同一张图上.
这里举一个最简单的例子, 将刚刚计算得到的频谱图的分贝值全部减10, 假设这就是原波形的下一等长时间的波形, 我们将这两张图画在一起.变成一个三维的图像.

1
2
3
4
5
6
fig, axes = plt.subplots(figsize=(20, 10))
mel_data_double = torch.stack((mel_data, mel_data-10))

im = axes.imshow(mel_data_double.T, aspect="auto", origin="lower", cmap="hot", extent=[1, 2, 0, 25])
cbar = fig.colorbar(im, ax=axes)
cbar.set_label("dB")

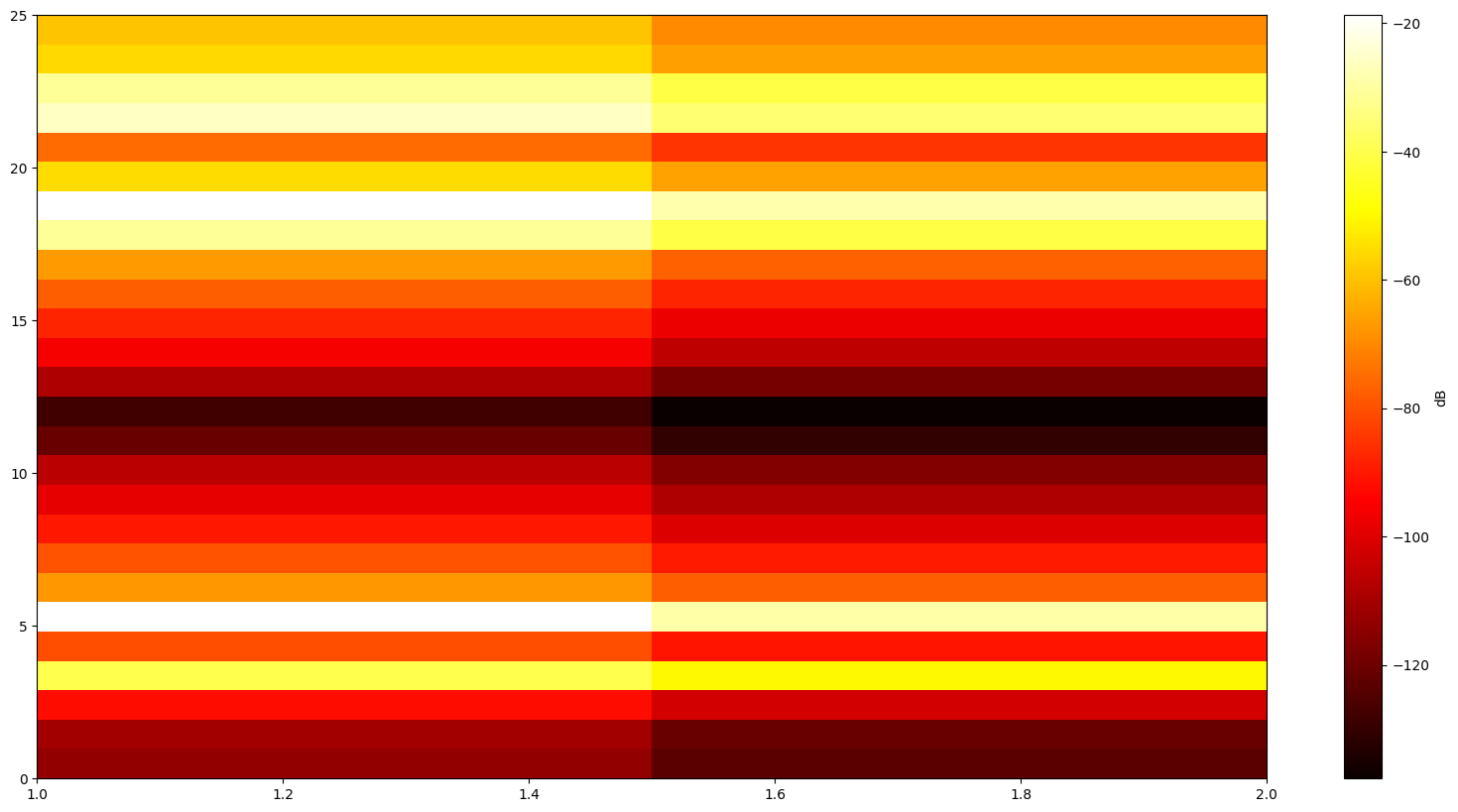
alt text
看不懂图先别慌, 横坐标[1, 2], 代表我们画了两个时刻的频谱图, 每一列代表一个时刻(也就是一帧), 纵坐标代表26 的频率部分, 而颜色代表对数比例的数值, 颜色越亮数值越大.

** 必要内容结束 **

加窗

首先窗函数长这样, 它的横坐标长度就是FFT 前原始采样波形的长度. 加窗就是将窗函数乘上采样波形, 对采样波形进行缩放.
目的就是减少频谱泄露:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 正弦波的频率
f1 = 500
# 周期
T = 1 / f1
# 采样范围
TT = 5*T
# 采样率
fs = f1 * 10
# 采样点数
N = int(fs * TT)

x = torch.linspace(0, TT, N)
y = 100 * torch.sin( (2*torch.pi)*f1*x)

fig, axes = plt.subplots(3, 1, figsize=(20, 5))

# 原波形
axes[0].plot(y)

# 窗函数
hann_window = torch.windows.hann(len(y))
axes[1].plot(hann_window)

# 相乘（加窗）
axes[2].plot(hann_window * y)

alt text